HVOF Modeling
In recent years a major trend in the thermal spray industry has been that of increasing the powder particle velocity in order to obtain better coating thickness and machinability, as well as improvements in hardness, density and wear resistance. Of the continually emerging new techniques, one that has been brought to a stage of industrial utilization is the HVOF process. In the HVOF process, combustion is used to heat the gas and the particles and a converging-diverging (de Laval) nozzle is used to accelerate them to high velocities. The gas, with its high velocity and density (relative to the plasma spraying process), accelerates the particles to significantly higher speed, thereby producing higher density coatings. As with any thermal spray process, the objective of HVOF technology is to transfer energy, both kinetic and thermal, to the powder particles with a high degree of efficiency. The physical and chemical conditions of the particle that impinge on the surface is dependent on a large number of parameters such as torch design, the gas jet conditions (temperature, velocity, pressure), particle size, material, and particle injection method.
Numerical modelling of the HVOF process
To advance the technology of the thermal spray system and improve the quality and efficiency of thermal spray coating, optimization of the coating properties is essential. Mathematical modelling of such a process is rather challenging because it involves complex physical phenomena of turbulent multi-phase flow. In addition, the flow regime varies from incompressible (with very low Mach numbers) to highly compressible flow (Mach number ~2.0). In general, two-phase flows are too complex to be treated in a complete way. There are two approaches commonly used to predict particulate two-phase flows. The Lagrangian or tracking approach treats the particles as discrete entities in a turbulent flow field and their trajectories are calculated. The other approach is the Eulerian or two-fluid model. In this approach, the cloud of particles is regarded as a continuum, and the particles pass through fixed differential control volumes. Both approaches have their own advantages and disadvantages, depending on the nature of the fluid particle flow. The Lagrangian particle tracking, is a reasonable method for solving the dilute flows in which, the particle motion is controlled by the surface and body forces on the particle. On the other hand, for a dense flow in which, the particle motion is controlled by the particle-particle interactions, the Eulerian approach is more descriptive of the physical phenomena. For a typical HVOF operating condition, the overall loading (the ratio of the mass flows of the dispersed to continuous phase) is about 10-20% and local loading is about 200-400%, which is rather high. Therefore, the two-phase flow in the HVOF process is a combination of dilute and dense flows. A 2-D axisymmetric model using the Lagrangian approach was developed. The flow was compressible and a k-epsilon turbulence model was used which included compressibility correction terms. Combustion was modeled by a multi-reaction Eddy Dissipation Model (EDM) that included the dissociation of the combustion products. Particles were modeled by a lumped-heat-capacity system. Using the Eulerian framework whereby most of the physical aspects of the particle-particle interactions in the HVOF process can be incorporated is to be developed soon.
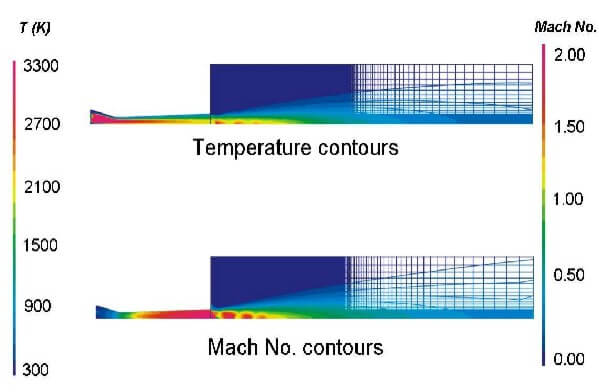
Figure 1

Figure 2
Results
Because of the three coaxial streams, including one reacting stream, the flow is extremely non-uniform in the converging part of the nozzle. Gas Mach number contours (Figure 1) show the sonic flow at the throttle and the supersonic flow in the diverging part of the gun. The shock diamonds appear after the flow leaves the torch. show the effect of shock diamonds on the temperature field. The shock diamonds play an important role in increasing the velocity and temperature of particles after they exit the gun.
The temperature and velocity profiles of 15 micron stainless steel particles (Figure 2) show the effects of shock diamonds.


